Jumlah Riemann pada Integral ini pertama kali diperkenalkan oleh Bernhard Riemann, seorang matematikawan asli Jerman. Lebih lengkap tentang Riemann bisa dibaca dalam Biografi Bernhard Riemann.
Mengenai bentuk aplikasi jumlah Riemann ini bisa untuk awalnya anda perhatikan kurva di bawah ini.
Permasalahannya adalah ketika anda disuruh menghitung luas area yang berwarna abu-abu?
Contoh aplikasi atau penggunaan pendekatan ini akan diawali dengan membagi area tersebut menjadi beberapa persegi panjang. Perhatikan gambar di bawah ini,
Masing masing Persegipanjang bisa dihitung luasnya dengan penjabaran
Persegi panjang 1 memiliki luas $ A_1 \, $ dengan panjang $\Delta x_1 \, $ dan lebar $ f(x_1) $ .
dengan $ A_1 = p \times l = f(x_1) \Delta x_1 $
Persegi panjang 2 memiliki luas $ A_2 \, $ dengan panjang $\Delta x_2 \, $ dan lebar $ f(x_2) $ .
dengan $ A_2 = p \times l = f(x_2) \Delta x_2 $
Persegi panjang 3 memiliki luas $ A_3 \, $ dengan panjang $\Delta x_3 \, $ dan lebar $ f(x_3) $ .
dengan $ A_3 = p \times l = f(x_3) \Delta x_3 $
dst
Persegi panjang 8 memiliki luas $ A_8 \, $ dengan panjang $\Delta x_8 \, $ dan lebar $ f(x_8) $ .
dengan $ A_8 = p \times l = f(x_8) \Delta x_8 $
Dengan menggunakan notasi sigma akan diperoleh,
$ \begin{align} A_1 + A_2 + A_3 + ... + A_8 & = f(x_1) \Delta x_1 + f(x_2) \Delta x_2 + f(x_3) \Delta x_3 + ... + f(x_8) \Delta x_8 \\ & = \displaystyle \sum_{i=1}^8 f(x_i) \Delta x_i \end{align} $
Defenis Jumlah Riemann
Jadi Jumlah Riemann bisa didefeniskan
Nilai $ \displaystyle \sum_{i=1}^n f(x_i) \Delta x_i \, $ didefenisikan sebagai Jumlah Riemann fungsi $ f(x) \, $ dimana $ x_i \, $ adalah titik wakil pada interval ke-$i \, $ dan $ \Delta x_i \, $ lebar interval ke-$i \, $ dan $ n \, $ banyak sub-interval (banyaknya persegi panjang yang terbentuk) dari interval $[a,b]$ . Titik wakil $(x_i) \, $ kita peroleh dengan tiga cara yaitu titik ujung kiri subinterval, titik tengah subinterval, dan titik ujung kanan subinterval, dimana setiap jenis titik wakil memberikan hasil yang berbeda. Untuk memahami lebih lanjut berikut beberapa contoh soal dan pembahasan yang saya kutip dari http://www.freemathlearn.tk/2014/03/pembahasan-jumlah-riemann-pada-integral.html
Contoh Soal dan Pembahasan Jumlah Integral Riemaan
Soal 1: Tentukan jumlah Riemann dari Fungsi di bawah ini,
 |
| Soal dari www.freemathlearn.tk |
Pembahasan:
Persegi panjang I : p = 0,7 , titik wakil $ x_1 = 0,5 \, $
sehingga lebar $ \, = f(x_1) = f(0,5) = (0,5)^2 - 4 (0,5) + 3 = 1,25 $ . $ L_1 = p \times l = 0,7 \times 1,25 = 0,875 $
Persegi panjang 2 : panjang = 1,7 - 0,7 = 1 , titik wakil $ x_2 = 1,5 \, $
sehingga lebar $ \, = f(x_2) = f(1,5) = (1,5)^2 - 4 (1,5) + 3 = -0,75 = 0,75 $ .
$ L_2 = p \times l = 1 \times 0,75 = 0,75 $
Persegi panjang 3 : panjang = 2,7 - 1,7 = 1 , titik wakil $ x_3 = 2 \, $
sehingga lebar $ \, = f(x_3) = f(2) = (2)^2 - 4 (2) + 3 = -1 = 1 $ .
$ L_3 = p \times l = 1 \times 1 = 1 $
Persegi panjang 4 : panjang = 4 - 2,7 = 1,3 , titik wakil $ x_4 = 3,5 \, $
sehingga lebar $ \, = f(x_4) = f(3,5) = (3,5)^2 - 4 (3,5) + 3 = 1,25 $ .
$ L_4 = p \times l = 1,3 \times 1,25 = 1,625 $
Jadi, Jumlah riemann atau pendekatan luasnya $ \, = L_1 + L_2 + L_3 + L_4 = 0,875 + 0,75 + 1 + 1,625 = 4,25 $
Soal 2. Diketahui suatu fungsi $ f(x) = x $ pada interval [0, 3], tentukan jumlah Riemann dengan menggunakan 6 subinterval sama panjang dan titik wakilnya :
a. titik ujung kanan subinterval
b. titik tengah subinterval
c. titik ujung kiri subinterval
Penyelesaian :
a). titik ujung kanan subinterval
Menentukan panjang setiap subinterval $(\Delta x_i ) $ :
Pada interval [0,3] dibagi menjadi 6 subinterval sama panjang, sehingga :
$ \Delta x_i = \Delta x = \frac{3-0}{6} = \frac{3}{6} = 0,5 $
Untuk dapat menentukan jumlah Riemann fungsi $ f(x) = x $ dengan 6 subinterval pada selang [0,3], perhatikan grafik fungsi $ f(x) = x $ pada interval [0, 3] dan titik ujung kanan subinterval, berikut:

Karena yang diminta adalah titik ujung kanan subinterval, maka nilai $ x_i \, $ yang digunakan adalah sebelah kanan setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0,5 \rightarrow f(x_1) = f(0,5) = 0,5 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 1 \rightarrow f(x_2) = f(1) = 1 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1,5 \rightarrow f(x_3) = f(1,5) = 1,5 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 2 \rightarrow f(x_4) = f(2) = 2 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2,5 \rightarrow f(x_5) = f(2,5) = 2,5 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 3 \rightarrow f(x_6) = f(3) = 3 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0,5 + 1 + 1,5 + 2 + 2,5 + 3 ] \times 0,5 \\ & = [ 10,5 ] \times 0,5 \\ & = 5,25 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 5,25.
b). titik tengah subinterval
Untuk dapat menentukan jumlah Riemann fungsi $ f(x) = x $ dengan 6 subinterval pada selang [0,3], perhatikan grafik fungsi $ f(x) = x $ pada interval [0, 3] dan titik tengah subinterval, berikut:

Karena yang diminta adalah titik tengah subinterval, maka nilai $ x_i \, $ yang digunakan adalah nilai tengah setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0,25 \rightarrow f(x_1) = f(0,25) = 0,25 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 0,75 \rightarrow f(x_2) = f(0,75) = 0,75 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1,25 \rightarrow f(x_3) = f(1,25) = 1,25 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 1,75 \rightarrow f(x_4) = f(1,75) = 1,75 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2,25 \rightarrow f(x_5) = f(2,25) = 2,25 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 2,75 \rightarrow f(x_6) = f(2,75) = 2,75 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0,25 + 0,75 + 1,25 + 1,75 + 2,25 + 2,75 ] \times 0,5 \\ & = [ 9 ] \times 0,5 \\ & = 4,5 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 4,5.
c). titik ujung kiri subinterval
Untuk dapat menentukan jumlah Riemann fungsi $ f(x) = x $ dengan 6 subinterval pada selang [0,3], perhatikan grafik fungsi $ f(x) = x $ pada interval [0, 3] dan titik ujung kiri subinterval, berikut:

Karena yang diminta adalah titik ujung kanan subinterval, maka nilai $ x_i \, $ yang digunakan adalah sebelah kiri setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0 \rightarrow f(x_1) = f(0) = 0 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 0,5 \rightarrow f(x_2) = f(0,5) = 0,5 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1 \rightarrow f(x_3) = f(1) = 1 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 1,5 \rightarrow f(x_4) = f(1,5) = 1,5 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2 \rightarrow f(x_5) = f(2) = 2 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 2,5 \rightarrow f(x_6) = f(2,5) = 2,5 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0 + 0,5 + 1 + 1,5 + 2 + 2,5 ] \times 0,5 \\ & = [ 7,5 ] \times 0,5 \\ & = 3,75 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 3,75.
Soal 3. Misalkan diketahui suatu fungsi $ f(x) = x^2 $ pada interval [0, 3], tentukan jumlah Riemann dengan menggunakan 6 subinterval sama panjang dan titik ujung kanan subinterval sebagai titik wakil tiap-tiap subinterval.
Penyelesaian :
*). Menentukan panjang setiap subinterval $(\Delta x_i ) $ :
Pada interval [0,3] dibagi menjadi 6 subinterval sama panjang, sehingga :
$ \Delta x_i = \Delta x = \frac{3-0}{6} = \frac{3}{6} = 0,5 $
*). Menentukan titik wakil $(x_i) $ dengan membagi menjadi 6 subinterval :
Karena yang diminta adalah titik ujung kanan subinterval, maka nilai $ x_i \, $ yang digunakan adalah sebelah kanan setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x^2 $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0,5 \rightarrow f(x_1) = f(0,5) = 0,5^2 = 0,25 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 1 \rightarrow f(x_2) = f(1) = 1^2 = 1 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1,5 \rightarrow f(x_3) = f(1,5) = 1,5^2 = 2,25 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 2 \rightarrow f(x_4) = f(2) = 2^2 = 4 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2,5 \rightarrow f(x_5) = f(2,5) = 2,5^2 = 6,25 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 3 \rightarrow f(x_6) = f(3) = 3^2 = 9 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0,25 + 1 + 2,25 + 4 + 6,25 + 9 ] \times 0,5 \\ & = [ 22,75 ] \times 0,5 \\ & = 11,375 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 11,375.
Perhatikan ketiga gambar luasan berikut ini.
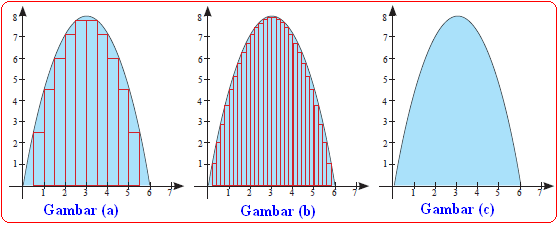
Luas Suatu Daerah dengan Jumlah Riemann
Misalkan kita akan menghitung luas suatu daerah yang dibatasi oleh kurva $ y = f(x) \, $ pada selang interval [a,b] dengan membagi menjadi $ n \, $ subinterval ($n \, $ menuju tak hingga), maka akan kita peroleh luas sebenarnya dengan perhitungan :
Luas $ \, = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $
dengan $ \Delta x_i = \Delta x = \frac{b-a}{n} $ .
penulisan lainnya : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_a^b f(x) dx \, $
Catatan :
Bentuk $ \int \limits_a^b f(x) dx \, $ inilah yang disebut sebagai integral Tentu fungsi $ f(x) \, $ pada interval [a,b] .
Luas $ \, = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $
dengan $ \Delta x_i = \Delta x = \frac{b-a}{n} $ .
penulisan lainnya : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_a^b f(x) dx \, $
Catatan :
Bentuk $ \int \limits_a^b f(x) dx \, $ inilah yang disebut sebagai integral Tentu fungsi $ f(x) \, $ pada interval [a,b] .
Untuk memudahkan dalam pengerjaan jumlah riemann, sebaiknya kita pelajari rumus umum notasi sigma berikut ini :
i). $ \displaystyle \sum_{k=1}^{n} \, k = 1 + 2 + 3 + ... + n = \frac{1}{2}n(n+1) $
ii). $ \displaystyle \sum_{k=1}^{n} \, k^2 = 1^2 + 2^2 + 3^2 + ... + n^2 = \frac{1}{6}n(n+1)(2n+1) $
iii). $ \displaystyle \sum_{k=1}^{n} \, k^3 = 1^3 + 2^3 + 3^3 + ... + n^3 = \left( \frac{1}{2}n(n+1) \right)^2 $
Contoh Soal Luas Daerah dengan Riemann :
Soal 1. Misalkan diberikan suatu fungsi $ f(x) = x $, tentukan integral tentu dari $ f(x) = x $ pada interval [0, 3] atau $ \int \limits_0^3 x dx $
Penyelesaian :
*). Interval yang diminta [a,b]=[0,3]
*). Menentukan nilai $ \Delta x_i = \Delta x = \frac{b-a}{n} = \frac{3-0}{n} = \frac{3}{n} $
*). Menentukan bentuk umum dari $ f(x_i) $
$ x_1 = 0 + \Delta x = 0 + \frac{3}{n} = \frac{1 \times 3}{n} $
$ x_2 = 0 + 2\Delta x = 0 + \frac{2 \times 3}{n} = \frac{2 \times 3}{n} $
$ x_3 = 0 + 3\Delta x = 0 + \frac{3 \times 3}{n} = \frac{3 \times 3}{n} $
dan seterusnya ........
$ x_i = 0 + i \Delta x = 0 + \frac{i \times 3}{n} = \frac{i \times 3}{n} $
Untuk bentuk $ f(x) = x \, $ , maka $ f(x_i) = \frac{i \times 3}{n} $
*). Menentukan jumlah riemann :
$ \begin{align} \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{i \times 3}{n} \frac{3}{n} \\ & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n i \times \frac{9}{n^2} \\ & = \displaystyle \lim_{n \to \infty} \frac{9}{n^2} \sum_{i=1}^n i \, \, \, \, \, \, \text{(gunakan rumus notasi sigma)} \\ & = \displaystyle \lim_{n \to \infty} \frac{9}{n^2} [\frac{1}{2}n(n+1)] \\ & = \displaystyle \lim_{n \to \infty} \frac{\frac{9}{2}n(n+1)}{n^2} \\ & = \displaystyle \lim_{n \to \infty} \frac{\frac{9}{2}n^2 + \frac{9}{2}n }{n^2} \\ & = \frac{9}{2} \end{align} $
Sehingga nilai dari $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_0^3 x dx = \frac{9}{2} $
Soal 2. Misalkan diberikan suatu fungsi $ f(x) = x^2 $, tentukan integral tentu dari $ f(x) = x^2 $ pada interval [0, 2] atau $ \int \limits_0^2 x^2 dx $
Penyelesaian :
*). Interval yang diminta [a,b]=[0,2]
*). Menentukan nilai $ \Delta x_i = \Delta x = \frac{b-a}{n} = \frac{2-0}{n} = \frac{2}{n} $
*). Menentukan bentuk umum dari $ f(x_i) $
$ x_1 = 0 + \Delta x = 0 + \frac{2}{n} = \frac{1 \times 2}{n} $
$ x_2 = 0 + 2\Delta x = 0 + \frac{2 \times 2}{n} = \frac{2 \times 2}{n} $
$ x_3 = 0 + 3\Delta x = 0 + \frac{3 \times 2}{n} = \frac{3 \times 2}{n} $
dan seterusnya ........
$ x_i = 0 + i \Delta x = 0 + \frac{i \times 2}{n} = \frac{i \times 2}{n} $
Untuk bentuk $ f(x) = x^2 \, $ , maka $ f(x_i) = \left( \frac{i \times 2}{n} \right)^2 = \frac{4}{n^2} \times i^2 $
*). Menentukan jumlah riemannya :
$ \begin{align} \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{4}{n^2} \times i^2 \frac{2}{n} \\ & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n i^2 \times \frac{8}{n^3} \\ & = \displaystyle \lim_{n \to \infty} \frac{8}{n^3} \sum_{i=1}^n i^2 \, \, \, \, \, \, \text{(gunakan rumus notasi sigma)} \\ & = \displaystyle \lim_{n \to \infty} \frac{8}{n^3} \frac{1}{6}n(n+1)(2n+1) \\ & = \displaystyle \lim_{n \to \infty} \frac{8}{n^3} \frac{1}{6}(2n^3 + 3n^2 + n) \\ & = \displaystyle \lim_{n \to \infty} \frac{4}{n^3} \frac{1}{3}(2n^3 + 3n^2 + n) \\ & = \displaystyle \lim_{n \to \infty} \frac{8n^3 + 12n^2 + 4n}{3n^3} \\ & = \frac{8 }{3 } \end{align} $
Sehingga nilai dari $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_0^2 x^2 dx = \frac{8}{3} $
6). Nyatakan limit berikut sebagai suatu integal tentu :
a). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \sqrt{\frac{4i}{n}} \frac{4}{n} $
b). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \left( 1 + \frac{2i}{n} \right) \frac{2}{n} $
c). $ \displaystyle \lim_{n \to \infty} \frac{1}{n} \left( \cos (\frac{\pi}{n}) + \cos (\frac{2\pi}{n}) + \cos (\frac{3\pi}{n}) + ... + \cos (\frac{n\pi}{n}) \right) $
Penyelesaian :
a). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \sqrt{\frac{4i}{n}} \frac{4}{n} $
*). Berdasarkan rumus : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $ maka :
*). $ \Delta x_i = \frac{b-a}{n} = \frac{4}{n} \rightarrow b - a = 4 $
dengan $ a = 0 \, $ maka $ b - a = 4 \rightarrow b - 0 = 4 \rightarrow b = 4 $.
*). Bentuk $ x_i = i \Delta x_i = i \frac{4}{n} = \frac{4i}{n} $
$ f(x_i) = \sqrt{\frac{4i}{n}} = \sqrt{x_i} \, $ artinya $ f(x) = \sqrt{x} $.
*). Bentuk integral tentunya :
$ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \sqrt{\frac{4i}{n}} \frac{4}{n} = \int \limits_a^b f(x) dx = \int \limits_0^4 \sqrt{x} dx $
Jadi, bentuk integral tentunya adalah $ \int \limits_0^4 \sqrt{x} dx $ .
b). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \left( 1 + \frac{2i}{n} \right) \frac{2}{n} $
Dari soal ini, bentuk $ 1 + \frac{2i}{n} \, $ , artinya $ x_i = a + i \Delta x_i \, $ , sehingga $ a = 1 $
*). Berdasarkan rumus : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $ maka :
*). $ \Delta x_i = \frac{b-a}{n} = \frac{2}{n} \rightarrow b - a = 2 $
dengan $ a = 1 \, $ maka $ b - a = 2 \rightarrow b - 1 = 2 \rightarrow b = 3 $.
*). Bentuk $ x_i = a + i \Delta x_i = 1 + i \frac{2}{n} = 1 + \frac{2i}{n} $
$ f(x_i) = \left( 1 + \frac{2i}{n} \right) = (x_i) \, $ artinya $ f(x) = x $.
*). Bentuk integral tentunya :
$ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \left( 1 + \frac{2i}{n} \right) \frac{2}{n} = \int \limits_a^b f(x) dx = \int \limits_1^3 x dx $
Jadi, bentuk integral tentunya adalah $ \int \limits_1^3 x dx $ .
c). $ \displaystyle \lim_{n \to \infty} \frac{1}{n} \left( \cos (\frac{\pi}{n}) + \cos (\frac{2\pi}{n}) + \cos (\frac{3\pi}{n}) + ... + \cos (\frac{n\pi}{n}) \right) $
*). Kita jadikan bentuk notasi sigma :
$ \displaystyle \frac{1}{n} \left( \cos (\frac{\pi}{n}) + \cos (\frac{2\pi}{n}) + \cos (\frac{3\pi}{n}) + ... + \cos (\frac{n\pi}{n}) \right) = \displaystyle \sum_{i=1}^n \frac{1}{n} \cos \pi (\frac{i}{n}) $
*). Sehingga soal yang akan kita ubah adalah $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{1}{n} \cos \pi (\frac{i}{n}) $
*). Berdasarkan rumus : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $ maka :
*). $ \Delta x_i = \frac{b-a}{n} = \frac{1}{n} \rightarrow b - a = 1 $
dengan $ a = 0 \, $ maka $ b - a = 1 \rightarrow b - 0 = 1 \rightarrow b = 1 $.
*). Bentuk $ x_i = i \Delta x_i = i \frac{1}{n} = \frac{i}{n} $
$ f(x_i) = \cos \pi (\frac{i}{n}) = \cos \pi (x_i) \, $ artinya $ f(x) = \cos \pi x $.
*). Bentuk integral tentunya :
$ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{1}{n} \cos \pi (\frac{i}{n}) = \int \limits_a^b f(x) dx = \int \limits_0^1 \cos \pi x dx $
Jadi, bentuk integral tentunya adalah $ \int \limits_0^1 \, \cos \pi x \, dx $ .


Jadilah Komentator Pertama untuk "Jumlah Riemann pada Integral (Integral Riemann)"
Post a Comment