Cara Menentukan Fungsi Naik dan Fungsi Turun

martha yunanda fungsi, Ilmu

Untuk menentukan sebuah fungsi naik atau sebuah fungsi turun dalam interval tertentu bisa digunakan turunan. Disinilah salah satu aplikasi turunan.

Fungsi naik adalah ketika sebuah fungsi beranjak ke menuju ke atas dari kiri bawah ke kanan atas. Sebalik pengertian dari fungsi turun, pada interval tertentu grafik fungsi bergerak dari kiri atas ke kanan bawah. Ketika perubahan fungsi dari naik ke turun terdapat titik yang dinamakan titik stasioner (maksimum). Sebaliknya, perubahan fungsi turun ke naik, terdapat titik yang dinamakan titik stasioner (minimum). Perhatikan ilustrasi di bawah ini,

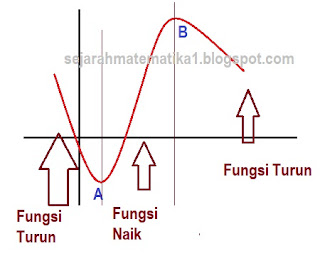A Titik Stasioner minimum, B titik Stasioner Maksimum

Cara menentukan fungsi naik dan fungsi turun mengikuti langkah berikut,

Langkah Menentukan Fungsi Naik dan Fungsi Turun

Misalkan kita memiliki fungsi f(x),
1) Carilah Turunan Pertama atau kita tentukan f’(x)
2) Carilah nilai x untuk f’(x) = 0
3) Ambil sebarang nilai a dan b dimana a<x dan b> x. Subtitusikan ke f'(x). Jika nilainya positif = fungsi naik. Jika nilai negatif = fungsi turun.

Lebih jelas dalam pengunaan langkah menentukan fungsi naik dan fungsi turun, kita akan aplikasi dalam bentuk contoh soal dan pembahasan.

Soal dan Pembahasan Fungsi Naik dan Fungsi Turun

#Soal 1: Diketahui fungsi f(x) = 3x² -18x+5. Tentukan nilai stasioner, Titik Stasioner dan Jenis Nilai Stasioner dari Fungsi tersebut.

Pembahasan:
Langkah (1):
f(x) = 3x² -18x+5
f’(x) = 6x -18

Langkah (2):
f’(x)= 0
6x-18 = 0
x =3

Langkah (3):
x<3 , kita ambil a =0. f'(0)=-18 (Nilai negatif = fungsi turun)
x> 3, kita ambil b = 4. f'(4) = 6 (Nilai Positif = fungsi naik)

Jadi kesimpulannya, Fungsi Naik pada interval x>3 dan turun pada selang x<3.

#Soal 2: Diketahi fungsi g(x) = 2x³ -3x²-12x+ 1. Hitunglah nilai stasioner dan tentukan jenisnya beserta titik stasioner fungsi tersebut.

Pembahasan:
Langkah (1):
g(x) = 2x³ -3x²-12x+ 1
g'(x) = 6x²-6x- 12

Langkah (2):
g'(x)=0
 6x²-6x- 12=0
 x²-x- 2=0
(x-2)(x+1) =0
x₁=2 , x₁=-1

Langkah (3):
Karena terdapat 2 nilai x, maka kita akan uji dalam bentuk interval. -1 <x<2.
Disini artinya kita akan uji 3 daerah. Daerah x<-1 , x antara -1 dan 2, x besar dari 2.
x<-1, kita ambil -2. g'(-2) =  24. (Positif = fungsi naik)
x antara -1 dan 2, kita ambil 0. g'(0) =-12 (negatif = fungsi turun)
x> 2, kita ambil 3. g'(3) =24. (positif = fungsi turun).

Jadi kesimpulannya Fungsi Naik pada Interval x<-1 ; x >2. Fungsi turun pada -1<x<2. Selanjutnya: Titik Belok dan Kecekungan Fungsi

Share on Facebook

Share on Twitter

Share on LinkedIn