Penyusutan harga beli adalah penyusutan dengan besaran yang tetap dari waktu ke waktu. Ini lebih dekat seperti barisan/deret aritmatika. Asumsikan sebuah barang dibeli dengan harga A, dan oersentase penyusutan i % , maka harga barang tersebut (nilai buku) pada periode ke n adalah Sn dan dapat dihitung menggunakan rumus:
$ S_n = A(1 - n p) $Ket
$ S_n = \, $ nilai buku akhir periode ke-n
$ A = \, $ harga beli (harga mula mula).
$ n = \, $ lama periode
$ p = \, $ persenpenyusutan dengan $ p = i\% $
Contoh Soal dan Pembahasan Penyusutan Harga Beli
Soal 1:
Sebuah mesin penghancur kertas dibeli dengan seharga Rp3.000.000,00. Hitung berapa nilai buku mesin tersebut pada akhir tahun ke-2, ke-5, dan ke-9 bila diasumsikan besar penyusutan adalah 3% /tahun dari harga belinya dan juga buatlah daftar penyusutan lengkap dengan akumulasinya!
Penyelesaian :
Diketahui : A = 3.000.000, dan $ p = 3\% = 0,03 $.
Nilai buku (harga mesin setelah penyusutan) :
Akhir tahun ke-2, artinya $ n = 2 $ :
$ \begin{align} S_n & = A(1 - n p) \\ S_2 & = 3.000.000 \times (1 - 2 \times 0,03) \\ & = 3.000.000 \times (1 - 0,06) \\ & = 3.000.000 \times 0,94 \\ & = 2.820.000 \end{align} $
Akhir tahun ke-5, artinya $ n = 5 $ :
$ \begin{align} S_n & = A(1 - n p) \\ S_5 & = 3.000.000 \times (1 - 5 \times 0,03) \\ & = 3.000.000 \times (1 - 0,15) \\ & = 3.000.000 \times 0,85 \\ & = 2.550.000 \end{align} $
Akhir tahun ke-9, artinya $ n = 9 $ :
$ \begin{align} S_n & = A(1 - n p) \\ S_9 & = 3.000.000 \times (1 - 9 \times 0,03) \\ & = 3.000.000 \times (1 - 0,27) \\ & = 3.000.000 \times 0,73 \\ & = 2.190.000 \end{align} $
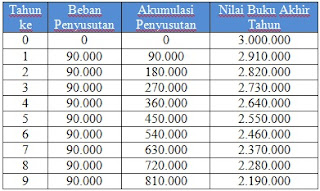
Daftar penyusutan lengkap
Beban penyusutan setiap periode (setiap tahun) :
$ = 3\% \times A = \frac{3}{100} \times 3.000.000 = 90.000 $
Soal 2:
Batman membeli mesin tik dengan harga Rp2.500.000,00. Berapa besar persentase penyusutan dan besarnya penyusutan setiap tahun menurut harga beli bila ditaksir mesin tik tersebut dalam 5 tahun bernilai Rp500.000,00?
Penyelesaian :
Diketahui : A = 2.500.000, $ n = 5 \, $ dan $ S_5 = 500.000 $.
Persentase penyusutan ($p$) :
$ \begin{align} S_n & = A(1 - n p) \\ S_5 & = 500.000 \\ 2.500.000 \times (1 - 5 \times \frac{i}{100}) & = 500.000 \\ (1 - 5 \times \frac{i}{100}) & = \frac{500.000}{2.500.000} \\ 1 - 5 \times \frac{i}{100} & = 0,2 \\ 5 \times \frac{i}{100} & = 1 - 0,2 \\ 5 \times \frac{i}{100} & = 0,8 \\ 5 i & = 0,8 \times 100 \\ 5 i & = 80 \\ i & = \frac{80}{5} = 16 \end{align} $
Persentase penyusutannya adalah 16% /tahun.
Penyusutan setiap tahun :
$ = 16\% \times A = \frac{16}{100} \times 2.500.000 = 400.000$
Jadi, Tiap tahun penyusutannya = Rp400.000,00
Soal 3:
Awal tahun 2010 PT Wonder Woman membeli sebuah Mobil Bekas dengan harga Rp15.000.000,00. Mobil tersebut menyusut 12,5% /tahun dari harga beli. Hitunglah
a. Nilai mobil pada awal tahun 2015!
b. Akumulasi penyusutan selama 6 tahun!
c. Umur dimana mobil tersebut tidak bernilai lagi!
Penyelesaian :
Diketahui : A = 15.000.000 dan $ p = 12,5\% = 0,125 $
Dari tahun 2010 sampai tahun 2015 = 5 tahun ($n = 5$)
$ \begin{align} S_n & = A(1 - n p) \\ S_5 & = 15.000.000 \times (1 - 5 \times 0,125) \\ & = 15.000.000 \times (1 - 0,625) \\ & = 15.000.000 \times 0,375 \\ & = 5.625.000 \end{align} $
Harga mobil tahun 2010 adalah Rp5.625.000,00.
Penyusutan selama 6 tahun,
Penyusutan setiap tahun = $ 12,5\% \times 15.000.000 = 1.875.000$
Penyusutan 6 tahun = $ 6 \times 1.875.000 = 11.250.000 $
Mobil tidak bernilai lagi, artinya nilai bukunya 0 ($ S_n = 0 $)
$ \begin{align} S_n & = A(1 - n p) \\ S_n & = 0 \\ A(1 - n p) & = 0 \, \, \, \, \, \, \, \text{(bagi A)} \\ 1 - n p & = 0 \\ 1 - n \times 12,5\% & = 0 \\ n \times 12,5\% & = 1 \\ n \times \frac{12,5}{100} & = 1 \\ n & = \frac{100}{12,5} \\ n & = 8 \end{align} $
Mobil tersebut tak bernilai lagi setelah 8 tahun.
Silakan baca juga penyusutan lainnya: Penyusutan Nilai Buku.
Jadilah Komentator Pertama untuk "Penyusutan Harga Beli"
Post a Comment