Aplikasi Fungsi Pembangkit dalam Masalah Counting

martha yunanda fungsi pembangkit, kombinatorika

Bentuk aplikasi dan penerapan fungsi pembangkit bisa digunakan dalam masalah counting. Contohnya dalam menemukan banyaknya solusi dari persamaan:
$x_1+x_2+x_3+...+x_n = C$,
C adalah konstanta.
dan x adalah bilangan positif dengan batas batas tertentu.

Sebagai contoh:
Tentukan banyak solusi dari
$\begin{align*} e_1+e_2+e_3=17 \end{align*}$
dimana $e_1, e_2, e_3$ adalah bilangan bulat non negatif dengan
$2 \leq e_1 \leq 5 \\ 3 \leq e_2 \leq 6 \\ 4 \leq e_3 \leq 7$

Jawab:
Banyaknya solusi pada batas interval masing masing e adalah koefisien $x^{17}$ dari ekspansi:
$\begin{align*} F(x)&=(x^2+x^3+x^4+x^5)(x^3+x^4+x^5+x^6)(x^4+x^5+x^6+x^7)\\ &=x^2(1+x+x^2+x^3)x^3(1+x+x^2+x^3)x^4(1+x+x^2+x^3)\\ &=x^9(\frac{(1-x^4}{1-x})^3)  \end{align*}$

Karena sudah ada $x^9$ terfaktorkan, sisanya anda harus menemukan $x^8$  (ingat $x^{17} = x^9.x^8$ ) dari $\frac{(1-x^4}{1-x})^3$
misal $g(x)=(\frac{1-x^4}{1-x})^3=(1-x^4)^3(1-x)^{-3}$
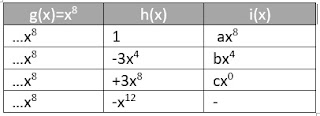
$h(x)=(1-x^4)^3=1-3x^4+3x^8-x^12$
$i(x) =(1-x)^{-3}$
Pada h(x) terdapat $x^0$ , $x^4$ , $x^{12}$
Agar g (x) menjadi $x^8$ maka

Akan dicari koefisien nilai a,b,c di atas. pada baris terakhir nilai i(x) tak dicari karena untuk pangkah h(x) saja sudah lebih dari 8.
Untuk $i(x) =(1-x)^{-3}$ disini anda gunakan, baca selengkapnya di Teorema Binomial Diperluas.
Rumus umum teorema binomial diperluas:

Misal untuk menghitung a, dari  $i(x) =(1-x)^{-3}$
k=8, n=3 , x=-x
maka
$(-1)^8 C (3+8-1,8)(-x)^8 = 1.45.x^8 = 45 x^8$
Jadi nilai a=45

Lanjutkan menghitung b dan c dan didapatkan hasil b=15 dan c= 1.
Sehingga

Total koefisien $x^8$ adalah 45+(-45)+3 = 3. Jadi banyak solusi untuk problem di atas adalah 3.

Share on Facebook

Share on Twitter

Share on LinkedIn