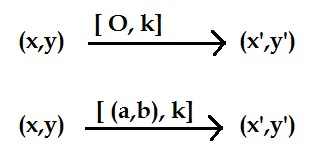 |
| Notasi dilatasi |
Dilatasi dengan Titik Pusat (0,0) [ O,k]
Titik acuan atau patokan diambil (0,0). Secara umum untuk mencari bayangan (x',y') dari titik asal (x,y) bisa digunakan rumus:
x' = kx dan y'= ky
k disini adalah faktor dilatasi atau perbesaran objek dilatasi. Untuk nilai |k| > 1 maka benda diperbesar. Untuk nilai 0<|k|<1 benda diperkecil. Berikut contoh soal dilatasi k dengan pusat O (0,0).
1) Dilatasi titik
Diketahui segitiga ABC dengan titik sudut A ( 2,3), B ( 7,1) dan C(-2,-5). Jika segitiga ABC di-dilatasi 3 dengan pusat O (0,0). Tentukan bayangan segitiga ABC atau A'B'C'. Hitunglah luas segitiga yang baru.
Penyelesaian soal ini sangatlah mudah, masing masin titik cukup dikalikan dengan faktor dilatasi yaitu 3. Maka akan diperoleh hasil A' ( 6,9) B' (21,3) dan C' (-6,-15). Untuk mencari luas segitiga, tanpa digambarkan bisa digunakan dibaca pada artikel : mencari luas bangun datar jika diketahui koordinat.
2) Dilatasi Persamaan Garis/Lingkaran/Kurva
Diketahui kurva y = x 2+5x-6. Jika kurva di dilatasi k = 2, tentukan persamaan kurva yang baru!
penyelesaian ini dimulai dengan menggunakan bentuk umum saja. Ingat x' = kx dan y'=ky. Untuk itu akan didapat persamaan berdasarkan soal x'=2x dan y'=2y. Jika diubah dalam bentuk x dan y akan didapat : x = 1/2 x' dan y = 1/2 y'. Dari x dan y tersebut kita substitusikan pada persamaan yang ada.
y = x 2 + 5x - 6 <==> (1/2 y') = (1/2 x') 2+ 5(1/2 x') - 6. Untuk perapihan selanjutnya silahkan dilanjutkan sendiri.
penyelesaian ini dimulai dengan menggunakan bentuk umum saja. Ingat x' = kx dan y'=ky. Untuk itu akan didapat persamaan berdasarkan soal x'=2x dan y'=2y. Jika diubah dalam bentuk x dan y akan didapat : x = 1/2 x' dan y = 1/2 y'. Dari x dan y tersebut kita substitusikan pada persamaan yang ada.
y = x 2 + 5x - 6 <==> (1/2 y') = (1/2 x') 2+ 5(1/2 x') - 6. Untuk perapihan selanjutnya silahkan dilanjutkan sendiri.
Contoh Soal Dilatasi (x,y) dengan pusat (a,b)
Titik acuan atau patokan diambil (a,b). Secara umum untuk mencari bayangan (x',y') dari titik asal (x,y) bisa digunakan rumus:
x' = k(x-a) + a dan y'= k(y-b)+b
k disini adalah faktor dilatasi atau perbesaran objek dilatasi. Untuk nilai |k| > 1 maka benda diperbesar. Untuk nilai 0<|k|<1 benda diperkecil. Berikut contoh soal dilatasi k dengan pusat O (a,b).
1) Dilatasi titik (x,y) dengan pusat (a,b)
Diketahui segitiga ABC dengan titik sudut A ( 2,3), B ( 7,1) dan C(-2,-5). Jika segitiga ABC di-dilatasi 3 dengan pusat M (1,3). Tentukan bayangan segitiga ABC atau A'B'C'. Hitunglah luas segitiga yang baru.
Penyelesaian : Nilai (a,b) adalah pusat dilatasi yaitu (1,3). kita akan gunakan rumus di atas. Sekarang ambil untuk titik A terlebih dahulu.
x' = 3(2-1) + 1 = 4 dan untuk y' = 3(3-1)+1 = 7. Jadi A' (4,7) Lakukan hal yang sama untuk titik B dan C. Silahkan dicoba sendiri sebagai latihan untuk anda.
Sementara untuk luas sama dengan saja dengan soal sebelumnya. Karena intinya untuk segitiga tersebu diperbesar 3 kali. Dimana pun posisinya tidaklah penting.
2) Dilatasi Persamaan Garis / Kurva / Lingkaran pusat (a,b)
Diketahui kurva y = x 2+5x-6. Jika kurva di dilatasi k = 2 yang berpusat di titik ( 2,-1) tentukan persamaan kurva yang baru!
penyelesaian ini dimulai dengan menggunakan bentuk umum saja. Ingat x' = k(x-a)+a dan y'=k(y-b)+b. Untuk itu akan didapat persamaan berdasarkan soal x'=2(x-2)+2 dan y'=2(y-(-1)) +(-1). Jika diubah dalam bentuk x dan y akan didapat : x = (x'+2)/2 dan y = (y'-1)/2. Dari x dan y tersebut kita substitusikan pada persamaan yang ada.
y = x 2 + 5x - 6 <==> ((y'-1)/2) = ( (x'+2)/2) 2+ 5( (x'+2)/2) - 6. Untuk perapihan selanjutnya menjadi tugas anda, karena saya hanya menjelaskan prinsip dilatasi, bukan menyelesaikan sebuah persamaan :).
Untuk mempermudah, sebenarnya telah ada kalkulator untuk menghitung dilatasi. Bisa anda lihat dan gunakan di : Kalkulator untuk Menghitung Transformasi Geometri.
penyelesaian ini dimulai dengan menggunakan bentuk umum saja. Ingat x' = k(x-a)+a dan y'=k(y-b)+b. Untuk itu akan didapat persamaan berdasarkan soal x'=2(x-2)+2 dan y'=2(y-(-1)) +(-1). Jika diubah dalam bentuk x dan y akan didapat : x = (x'+2)/2 dan y = (y'-1)/2. Dari x dan y tersebut kita substitusikan pada persamaan yang ada.
y = x 2 + 5x - 6 <==> ((y'-1)/2) = ( (x'+2)/2) 2+ 5( (x'+2)/2) - 6. Untuk perapihan selanjutnya menjadi tugas anda, karena saya hanya menjelaskan prinsip dilatasi, bukan menyelesaikan sebuah persamaan :).
Untuk mempermudah, sebenarnya telah ada kalkulator untuk menghitung dilatasi. Bisa anda lihat dan gunakan di : Kalkulator untuk Menghitung Transformasi Geometri.