Cara Menghitung Panjang Garis Bagi Segitiga

martha yunanda geometri

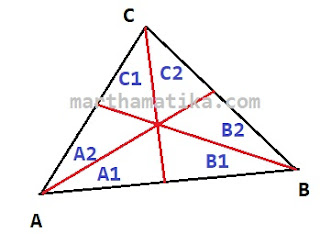
Selain garis tinggi dan garis berat, juga dikenal garis istimewa pada segitiga yakninya garis bagi. Pengertian dan defenisi garis bagi adalah garis yang ditarik dari salah satu sudut segitiga dan garis tersebut akan membagi sudut tersebut menjadi 2 sama besar. Berikut contoh gambar garis bagi segitiga,

Garis bagi ditunjukkan oleh garis yang bewarna merah. Masing masing membagi sudut A menjadi A1 dan A1 yang mana sama besar. Begitu juga dengan sudut B dan C.

Ada beberapa hal yang memenuhi sifat garis bagi segitiga,

• Ketiga garis bagi akan berpotongan pada satu titik pada segitiga di atas yaitunya titik O. Titik itu dinamakan titik bagi.
• Sisi didepan yang dibagi, perbandingan panjangnya sama dengan sisi yang berdekatan dengan bagian tersebut. Misal pada segitiga di atas. BD: DC = AB:AC (Baca Pembuktiannya di Sini)
• Jika dibuat sebuah lingkaran dalam segitiga, maka titik bagi akan menjadi titik pusat lingkaran tersebut.

Rumus Menghitung Garis Bagi pada segitiga

Untuk menentukan panjang garis bagi pada sebuah segitiga, anggap segitiga seperti gambar berikut,

$AD ^2 =AC.AB-BD.DC \\ BE^2 =AB.BC - AE-EC \\ FC^2 = BC.CA -AF.FB$

Sementara untuk sisi yang terbagi misal sisi:

$BD = \frac {AB}{AB+AC} \times BC \\ CD = \frac {AC}{AB+AC} \times  BC$

Begitu juga prinsipmya untuk menghitung DF, AF, AE dan EC.

Dalam pengaplikasian rumus tersebut, silakan lihat contoh soal dan pembahasan menentukan besar panjang garis bagi segitiga di bawah ini,

Contoh Soal 1.

Segitiga ABC siku-siku di A dengan panjang AB = 3 cm dan BC = 4 cm. Dari titik sudut A ditarik garis bagi AD. Tentukan panjang AD!

Pembahasan:

Segitiga yang dimaksud digambarkan,

Berdasar kan sifat ke-dua di atas: BD: DC = AB:AC  maka BD:CD =3:4.

Berdasarkan rumus menghitung BD dan CD bisa dihitung,

$BD = \frac{3}{7}.BC = \frac{3}{7}.5 = \frac{15}{7} $

$ CD = \frac{4}{7}.BC = \frac{4}{7}.5 = \frac{20}{7} $

Silakan terakhir dihitung AD dimana,

$ \begin{align} AD^2 & = AC.AB - BD.DC   \\  & = 4.3 - \frac{15}{7} . \frac{20}{7} \\ & = 12 - \frac{300}{49} \\ & = \frac{588}{49} - \frac{300}{49} \\ AD^2 & = \frac{288}{49} \\ AD  & = \sqrt{\frac{144.2}{49} } \\ AD  & = \frac{12}{7}\sqrt{2} \end{align} $

Jadi, panjang garis bagi $ AD \frac{12}{7}\sqrt{2} \, $ cm

Contoh Soal 2

Sebuah segitiga ABC dengan AB = 21 cm, BC = 18 cm, dan AC = 12 cm. CD adalah garis bagi. E adalah titik tengah BC. Hitunglah panjang DE!

Pembahasan:

Berdasarkan perbandingan: AD:BD= AC:BC maka AD:BD =18:12 = 3:2
Berdasarkan rumus menghitung AD dan BD diperoleh:
$ AD = \frac{3}{5}AB = \frac{3}{5}.21 = \frac{63}{5} \\  BD = \frac{2}{5}AB = \frac{2}{5}.21 = \frac{42}{5} $

Panjang CD dapat dihitung:
$ \begin{align} CD^2 & = CA.CB - AD.BD   \\ CD^2 & = 12.18 - \frac{63}{5} . \frac{42}{5} \\ CD^2 & = \frac{2754}{25} \end{align} $

Titik E berada di tengah BC, artinya DE adalah garis berat pada segitiga BDC.
Panjang garis berat DE pada segitiga BDC,(Silakan lihat postingan mengenai cara menghitung garis berat)
$ \begin{align} DE^2 & = \frac{1}{2}.CD^2 + \frac{1}{2}.DB^2 - \frac{1}{4}.BC^2 \\ DE^2 & = \frac{1}{2}. \frac{2754}{25} + \frac{1}{2}. (\frac{42}{5})^2 - \frac{1}{4}.12^2 \\ DE^2 & = \frac{1377}{25} + \frac{882}{25} - 36 \\ DE^2 & = \frac{2259}{25} - 36 \\ DE^2 & = \frac{2259}{25} - \frac{900}{25} \\ DE^2 & = \frac{1359}{25} = \frac{9 . 151}{25} \\ DE & = \sqrt{ \frac{9 . 151}{25} } \\ DE & = \frac{3}{5}\sqrt{ 151} \end{align} $
Jadi, panjang $ DE = \frac{3}{5}\sqrt{ 151} \, $ cm

Share on Facebook

Share on Twitter

Share on LinkedIn