Pembuktian Perbandingan Garis Berat pada Segitiga

martha yunanda geometri

Jika terdapat segitiga ABC dengan garis berat masing masing seperti pada gambar di bawah ini,

Maka berlaku

BO:OE = AO:OD = CO:OF = 2:1

Ini akan dibuktikan. Silakan dipahami pembuktiannya berikut,

Pembuktian ini dibutuhkan dalil menenlaus (BACA DALIL MENALAUS).
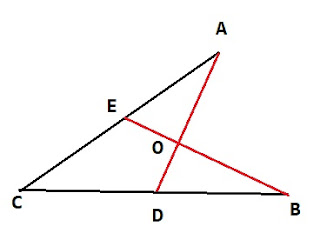
Perhatikan gambar potongan segitiga di bawah ini,

Pada gambar di atas berlaku dalil menenlaus,
Perbandingan AO : OD dengan $ \frac{AF}{FB} = 1 \, $ dan $ \frac{BC}{CD} = \frac{2}{1} $
$ \begin{align} \frac{DO}{OA}. \frac{AF}{FB}.\frac{BC}{DC} & = 1 \\ \frac{DO}{OA}. 1.\frac{2}{1} & = 1 \\ \frac{DO}{OA} & = \frac{1}{2} \\ \frac{AO}{OD} & = \frac{2}{1} \end{align} $

Perbandingan CO : OF dengan $ \frac{CD}{DB} = 1 \, $ dan $ \frac{BA}{FA} = \frac{2}{1} $
$ \begin{align} \frac{FO}{OC}. \frac{CD}{DB}.\frac{BA}{FA} & = 1 \\ \frac{FO}{OC}. 1.\frac{2}{1} & = 1 \\ \frac{FO}{OC} & = \frac{1}{2} \\ \frac{CO}{OF} & = \frac{2}{1} \end{align} $

Kemudian tinjau potongan segitiga dari sisi lain,

Di sini berlaku dalil menelaus sebagai berikut,
Perbandingan BO : OE dengan $ \frac{BD}{DC} = 1 \, $ dan $ \frac{CA}{EA} = \frac{2}{1} $
$ \begin{align} \frac{EO}{OB}. \frac{BD}{DC}.\frac{CA}{EA} & = 1 \\ \frac{EO}{OB}. 1.\frac{2}{1} & = 1 \\ \frac{EO}{OB} & = \frac{1}{2} \\ \frac{BO}{OE} & = \frac{2}{1} \end{align} $

Terbukti AO : OD = 2 : 1, BO : OE = 2 : 1, dan CO : OF = 2 : 1

Share on Facebook

Share on Twitter

Share on LinkedIn