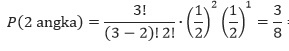- Dilakukan n -kali percobaan
- Untuk satu kali percobaan akan menghasilkan 2 kemungkinan saja. Misalkan - koin, pluang sukses atau gagal.
- Hasil percobaan tersebut harus saling bebas
- Semua peluang harus sama pada setiap percobaan.
Percobaan binomial yang dilakukan dan menghasilkan distribusi berupa peluang khusus. Inilah yang disebut dengan distribusi binomial. Pada percobaan binomial, hasilnya nanti dikelompokkan menjadi dua ; berhasil atau gagal. Misalnya ketika menjawab sebuah pertanyaan soal pilihan ganda. Jawaban yang benar termasuk kelompok 'berhasil'. Sementara untuk jawaban yang salah disebut kelompok 'gagal'. Sebelum melihat contoh soal dan pembahasan distribusi binomial ini harus disepakati penggunaan simbol. Berikut simbol atau notasi pada distribusi binomial yang sering digunakan
P(B)= Peluang berhasil, bisa juga dimisalkan dengan p
P(G) = Peluang gagal, bisa juga dimisalkan dengan q
n = banyak percobaan yang dilakukan
X = banyaknya percobaan yang berhasil nilai X ini berada 0<X<n.
Rumus Peluang Binomial
Ketika melakukan sebuah percobaan binomial. Peluang untuk mendapatkan X-kali berhasil bisa dinyatakan dengan rumus sebagai berikut.
Agar lebih mudah memahami langsung diperhatikan contoh soal distribusi normal berikut ini.
Contoh Soal dan Pembahasan Distribusi Binomial 1
Sebuah koin dilempar 3 kali pelemparan. Tentukan peluang didapatnya dua angka pada pelemparan tersebut.
Penyelesaian Biasa: Dengan cara biasa : Pada pelemparan tiga koin akan didapatkan ruang sampe sebagai berikut S={ GGG, GGA, GAG, AGG, AAG, AGA, GAA, AAA}. Dengan demikian terlihat bahwa peluang munculnya dua angka adalah 3 dari 8 buah kemngkinan. Ini bisa ditulis peluangnya 3/8.
Penyelesaian dengan distribusi binomial:
Bagaimana jika diselesaikan dengan binomial. Dalam hal ini kembali perhatikan syarat di atas. Kita akan mendapatkan n = 3 (banyak percobaan). Percobaan menghasilkan dua kemungkinan yaitu Angka atau Gambar. Peluang angka dan gambar sama sama 1/2. Semua kriteria binomial bisa dipenuhi, artinya kita bisa menggunakan penyelesaian dengan distribusi binomial di sini. Kembai pada hal yang diketahui, n=3 ; X =2 (diharapkan 2 Angka) ; p =1/2 dan q = 1/2, dimana p dan q peluang angka dan gambar masing masingnya. Berikutnya disubstitusikan pada rumus binomial yang telah diberikan sehingga akan menjadi
Jadi disini terlihat jelas bahwasanya hasil dengan cara sederhana akan sama dengan menggunakan distribusi binomial. Soal di atas sebagai bentuk pembuktian binomial saja. Penggunaan distribusi binomial sendiri untuk percobaan yang dilakukan yang angkanya (n) banyak sekali, misalkan 50. tidak mungkin untuk mendaftarkan semuan anggota ruang sampel.
Contoh 2:
Kemungkinan seorang balita tidak di imunisasi campak adalah 1/5. Pada tanggal 26 Juni 2016, di klinik Anda terdapat 4 orang balita. Berapakah peluang dari balita tersebut 2 orang belum mendapatkan imunisasi campak?
Penyelesaian:
Langsung kita selesaikan dengan polinomial. Identifikas terlebih dahulu. Total (n) = 4. Yang diinginkan/harapkan (x) = 2. p= 1/5. Karena p+q =1. Maka didapat q =1 -0,2 =0,8. Kemudian digunakan penyelesaian dengan menggunakan rumus distribusi binomial.
Itulah contoh soal dan pembahasan tentang distribusi binomial. Yang paling penting dipahami adalah bagaimana menentukan : n , x, p dan q. Jika sudah bisa mengidentifikasi hal tersebut maka untuk menghitung sangatlah mudah dengan menggunakan rumus yang telah ada.
Contoh 2:
Kemungkinan seorang balita tidak di imunisasi campak adalah 1/5. Pada tanggal 26 Juni 2016, di klinik Anda terdapat 4 orang balita. Berapakah peluang dari balita tersebut 2 orang belum mendapatkan imunisasi campak?
Penyelesaian:
Langsung kita selesaikan dengan polinomial. Identifikas terlebih dahulu. Total (n) = 4. Yang diinginkan/harapkan (x) = 2. p= 1/5. Karena p+q =1. Maka didapat q =1 -0,2 =0,8. Kemudian digunakan penyelesaian dengan menggunakan rumus distribusi binomial.