Bagian Lingkaran: Titik Kuasa dan Garis Kuasa Lingkaran

Pada bangun datar lingkaran dikenal istilah Kuasa Lingkaran, Titik Kuasa Lingkaran dan Garis Kuasa Lingkaran. Lantas, apa pengertian dari Kuasa, Titik Kuasa dan Garis kuasa lingkaran? Berikut akan diuraikan mengenai bagian bagian lingkaran tersebut.

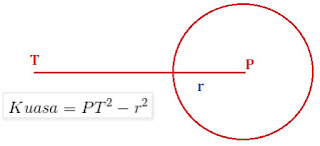
Jika dimisalkan sebuat titik T (x₁, y₁) berada di luar sebuah lingkaran. Sementara itu lingkaran memiliki pusat di titik P. Maka arti dari Kuasa lingkaran bisa didefenisikan sebagai:

Kuasa: PT²-r²

Lebih jelas, anda perhatikan gambar di bawah ini.

Sekarang kita akan lihat bagaimana jika dalam kasus persamaan sebuah lingkaran. Misalkan sebuah lingkaran dengan persamaan:

L : x² + y² +Ax + By + C = 0

Berdasarkan persamaan tersebut akan diketahui,

$ r^2 = \frac{1}{4}A^2 + \frac{1}{4}B^2 - C $

$ Pusat= \, \left( -\frac{A}{2}, - \frac{B}{2} \right) $

Maka Kuasa Lingkaran (K) dititik (T (x₁, y₁)) bisa dinyatakan secara matematis dengan rumus:

$ K = TP^2 - r^2 = \left( x_1 + \frac{1}{2}A \right)^2 + \left( y_1 + \frac{1}{2}B \right)^2 - r^2 \, $

Atau:

$ K = x_1^2 + y_1^2 +Ax_1 + By_1 + C $
(intinya: subtitusikan nilai x dan y ke persamaan Lingkaran)

Mungkin anda akan bertanya, apa guna Kuasa Lingkaran? Guna menentukan atau mencari kuasa lingkaran ini adalah untuk menentukan kedudukan atau posisi titik pada lingkaran. Ketentuan kedudukan atau posisi Kuasa lingkaran ini adalah:

Untuk K> 0, maka titik tersebut berada di luar lingkaran
Untuk K= 0, maka titik berada tepat pada perimeter lingkaran
K<0 maka titik berada di dalam lingkaran.

Sebagai contoh, Anda bisa menentukan titik (1,2) pada Lingkaran:

$ L_1: x^2 + y^2 +2x - 4y + 6 = 0 $

$ L_2: (x-2)^2 + (y + 1)^2 = 13 $

Sekarang anda subtitusikan nilai x=2 dan y=1 pada lingkaran:

$K_1: 1^2 + 2^2 +2.1 - 4.2 + 6 = 5 $

Karena K>0 maka titik tersebut berada di luar lingkaran

$K_2: (x-2)^2 + (y + 1)^2 = 13 \\ (x-2)^2 + (y + 1)^2 - 13= 0 \\ (1-2)^2 + (3 + 1)^2 - 13 = -3 $

Karena K< 0, artinya titik tersebut berada di dalam lingkaran.

Titik Kuasa, Garis Kuasa

Jika anda memiliki 2 buah lingkaran, himpunan semua titik yang memiliki kuasa sama dengan kedua lingkaran tersebut disebut titik-titik kuasa. Sementara itu, anda sudah mengetahui jika 2 titik Akan membentuk garis.

Jika semua titik tersebut dikumpulkan maka akan terbentuk garis. Nah, garis yang terbentuk tersebut dinamakan dengan garis kuasa. Ilustrasinya, anda perhatikan gambar di bawah ini,

Perlu dicatat, setiap garis kuasa selalu tegak lurus dengan garis yang menghubungkan ke dua pusat lingkaran.

Cara Menentukan Persamaan Garis Kuasa Lingkaran

Jika terdapat 2 lingkaran dengan persamaan:

$ L_1 : x^2 + y^2 + A_1x + B_1y + C_1 = 0 \, $
$ L_2 : x^2 + y^2 + A_2x + B_2y + C_2 = 0 $ .

Untuk mencari Garis kuasa dari Lingkaran tersebut adalah:
$ L_1 - L_2 = 0 \, $
$ \, (A_1 - A_2)x + (B_1 - B_2)y + (C_1 - C_2) = 0 $

Agar lebih mudah memahaminya anda bisa lihat contoh soal dan pembahasan mengenai Titik Kuasa dan Garis Kuasa.

Share on Facebook

Share on Twitter

Share on LinkedIn