Teorema Bintang David (Star of David Theorem)

martha yunanda faktamatika, Ilmu

Anda tentu tahu bentuk yang dinamakan dengan bintang David. Jika anda belajar geografi, maka akan anda temukan pada bendera Israel. Terlepas dari isu agama, ras, iluminati dan lainnya. Dalam matematika pernah diperkenalkan Teorema Bintang David.

Dikutip dari Mathworld Wolfram, Teorema Bintang David ini diperkenalkan oleh HW Gould di tahun 1972. Berikut dikembangangkan oleh beberapa ahli matematika pada tahun-tahun sesudahnya.

Apa bunyi Teorema Bintang David dan bagaimana aplikasinya? Berikut penjelasannya.

Teorema bintang David ini menjelaskan bahwasanya:
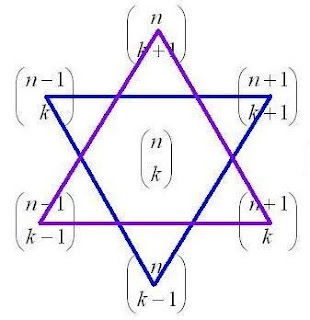
pembagi umum terbesar ${{n-1} \choose k}$, ${n \choose {k-1}}$, dan ${{n + 1} \choose {k + 1}}$ sama dengan pembagi umum terbesar ${{n-1} \choose {k-1}}$, ${n \choose {k + 1}}$, dan ${{n + 1} \choose k}$
Atau anda bisa perhatikan gambar di bawah ini,

Lalu kenapa ini disebut dengan dengana teorema Bintang David (teorema bintang Daud)?
Antara bagian pertama dihubungkan dengan segitiga biru.
 ${{n-1} \choose k}$, ${n \choose {k-1}}$, dan ${{n + 1} \choose {k + 1}}$

Sementara bagian ke-dua dihubungkan dengan segitiga ungu,
${{n-1} \choose {k-1}}$, ${n \choose {k + 1}}$, dan ${{n + 1} \choose k}$
Sehingga terbentuk bintang david.

CATATAN:
${n \choose {k}} = _nC_k$
*Kombinasi

Lalu atas dasar apa penyusunan n dan k tersebut? Penyusunan n dan k berbentuk umum seperti gambar di atas dilakukan berdasarkan segitiga Pascal. Sederhananya kita ambil contoh n=4 dan k =2. sesuai bagian 1
${{n-1} \choose k}$, ${n \choose {k-1}}$, dan ${{n + 1} \choose {k + 1}}$
(3,4,10)

Bagian 2
${{n-1} \choose {k-1}}$, ${n \choose {k + 1}}$, dan ${{n + 1} \choose k}$
(3,4,10)
 Jika digambarkan dalam segitiga Pascal bagian 1 dan bagian 2 tersebut akan membentuk,

Nah sesuai teorema bintang David, Pembagi terbesar (FPB) dari kedua bagian tersebut sama sama 1.

Tentu saja ini kurang menarik karena anda mengambil n=4 dan k=2. Angka yang anda peroleh kecil (3,4,10).

Agar lebih menantang sekarang untuk contoh berikutnya ambil n=10 dan k=7
Bagian 1
${{n-1} \choose k}$, ${n \choose {k-1}}$, dan ${{n + 1} \choose {k + 1}}$
 (36,210,165)

Bagian 2
${{n-1} \choose {k-1}}$, ${n \choose {k + 1}}$, dan ${{n + 1} \choose k}$
(84,45,330)

Posisi bagian tersebut pada segitiga Pascal sebagai berikut,

Berbentuk bintang David bukan? Sekarang anda cari FPB bilangan antara bilangan tersebut (Bisa Gunakan: Kalkulator Menghitung FPB). Barang pasti FPB bilangan bilangan tersebut adalah 3.

Sederhana sekali, sebuah bintang David yang menghubungkan bilangan bilangan pada segitiga Pascal, maka FPB bilangan tersebut sama. Atau bentuk umumnya bisa anda lihat pada gambar paling atas tadi.

Share on Facebook

Share on Twitter

Share on LinkedIn