Contoh Kejadian dalam Peluang Matematika
Ketika sebuah koin dilemparkan 20 kali. Tak ada alasan untuk memastikan sisi angka akan muncul lebih sering dari sisi gambar. Begitu juga sebaliknya, tak dapat dipastikan bahwa sisi gambar akan muncul lebih sering dari sisi angka. Andaikan, koin tersebut dilempar sebanyak sekian kali lemparan. Maka, sisi angka disebut memiliki peluang yang sama dengan sisi gambar. Ilustrasi tersebut menjelaskan peluang kejadian yang sama.
Kemudian, dilakukan percobaan lain, sebuah koin logam dilempar sebanyak n kali. Pada pengamatan yang dilakukan di satu sisi tertentu ( angka saja / gambar saja) ternyata muncul sebanyak k kali. Nilai perbandingan k dengan n (k/n) disebut frekuensi relatif. Apabila nilai k./n ini makin mendekati suatu nilai 1/2 (nilai peluang munculnya satu sisi secara teoritis) maka akan semakin mantap. Dasar kemantapan ini yang menjadi dasar dasar teori peluang (probability). Terkait : Sejarah Ditemukannya Peluang.
Pengertian peluang bisa ditarik dari ilustrasi berikut ini. Peluang (P) sebuah kejadian A adalah perbandingan antara banyak kejadian yang diharapkan dengan semua kemungkinan yang terjadi. Secara bahasa bisa dibilang sebagai : " yang diharapkan/ yang mungkin". Sederhannya begini, jika dari 10 wanita, diharapakan 1 wanita ingin dijadikan istri. Maka peluang wanita tersebut untuk dijadikan istri adalah : "yang diharapkan/ yang mungkin" = 1/10. Sekarang secara matematis peluang itu bisa ditulis.
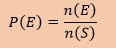 |
| Rumus Peluang |
P(E) = Peluang ; n(E) = banyak yang diinginkan; n(S) = semua yang ada. Sebagai contoh permasalahan di atasa tadi. maka diketahiu n(E) = 1 (1 orang yang dimau) n(S) = 10 (ada 10 orang semuanya). P (E) = 1/10.
Contoh Soal dan Penyelesaian Peluang
Sekarang agar lebih memahami peluang ini. Bisa dikerjakan contoh soal di bawah ini. Kerjakan sebisa-nya terlebih dahulu tanpa melihat pembahasan.
1) Sebuah dadu dilempar sekali. Berapa peluang munculnya angka dadu genap pada dadu tersebut?
2) Pada seperangkat kartu bridge, diambil satu kartu. berapa peluang terambilnya kartu King hitam.
3) Dalam sebuah kotak ada 10 buah kelereng yang terdiri dari 5 kelereng hijau, 3 kelereng merah dan 2 kelereng hitam. Jika diambil 3 kelereng sekaligus, berapa peluan terambilnya 2 kelereng hijau dan 1 kelereng hitam?
Pembahasan Soal Peluang
1) Pada sebuah dadu terdapat 6 kemungkinan yaitu {1,2,3,4,5,6}. Ingat semua kemungkinan = n (S) = 6. Sementara yang diinginkan adalah angka genap, angka genap tersebut {2,4,6}, artinya yang diharapkan = n (E) = 3. Sesuai rumus peluang maka : P(E) = n(E) / n(S) = 3/6 =1/2.
2) Seperangkat kartu bridge ada 52 kartu. Semua kemungkinan = n (S) = 52. Sementara yang diinginkan King Hitam ada 2 , n (E) = 2. Sesuai dengan rumus peluang maka P(E) = n(E)/ n(S) = 2/52 = 1/26.
3) Untuk soal nomor 3 ini harus menguasai terlebih dahulu tentang kombinasi. Baca di : Materi, Soal dan Pembahasan tentang Kombinasi. Cara pengambilan 2 kelereng hijau 5C2, sementara 1 kelereng hitam 2C1. Cara pengambilan total yang kiat harapkan adalah 5C2x2C1 = 20. Artinya yang diharapkan = n(E) = 20. Sementara yang mungkin itu semua dari 10 kelereng diambil 3 kelereng , 10C3 = 120. Semua kemungkinan adalah = n(S) = 120. Jadi peluangnya = 20/120.