Pengertian dan defenisi elips adalah terdapat 2 titik $f_1$ dan $f_2$ di suatu bidang. Elips didefeniskan adalah himpunan semua titk yang jaraknya terhadap $f_1$ dijumlahkan dengan $f_2$ selalu tetap atau konstan.
$d_1+d_2= k$.
Sementara $f_1$ dan $f_2$ dinaana dengan fokus. Perhatikan ilustrasi di bawah ini,
Terlihat pada animasi di atas, jarak $d_1+d_2$ selalu tetap dari posisi manapun.
Rumus luas Elips adalah:
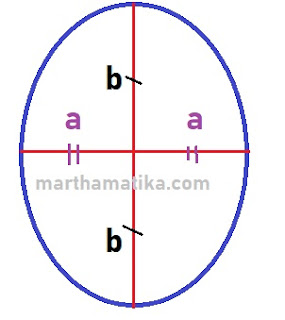
$L = \pi \times a \times b$Dimana a dan b adalah sumbu mayor dan sumbu minor. Atau bisa digambarkan sebagai berikut,
Bentuk umum persamaan elips:
$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \, $
Pembuktian Rumus Luas Elips
Perhatikan elips di bawah ini,
Terdapat elips pada sistem kordinat Cartesian. Pusat elips di titik (0,0) sehingga elips terbagi 4 bagian yang sama besar yang mana masing masing di kuadran 1,2,3 dan 4. Kita akan lihat bagian yang diarsir atau di kuadran 1.
Pembuktian rumus luas elips menggunakan prinsip integral (luas daerah dibawah kurva). Namun anda juga harus ingat beberapa identitas trigonometri, karena akan dibuktikan dengan sistem koordinat polar.
Identitas trigonometri
$ \cos ^2 \theta + \sin ^2 \theta = 1 \\ \cos ^2 \theta = 1 - \sin ^2 \theta $
Misal : $ x = a \sin \theta \, $
Bisa ditulis:
$ \begin{align} \sqrt{a^2 - x^2} & = \sqrt{a^2 - (a \sin \theta)^2} \\ & = \sqrt{a^2 - a^2 \sin ^2 \theta } \\ &= \sqrt{a^2 (1 - \sin ^2 \theta ) } \\ & = \sqrt{a^2 ( \cos ^2 \theta ) } \\ & = a \cos \theta \end{align} $
Turunan terhadap $ \theta $ bisa ditulis.
$ x = a \sin \theta \rightarrow \frac{dx}{d \theta } = a \cos \theta \rightarrow dx = a \cos \theta \, d \theta $
Sementara batas wilayah untuk integral dari daerah tersebut, [0,a].
$ x = a \sin \theta \rightarrow \sin \theta = \frac{x}{a} $
$ x = 0 \rightarrow \sin \theta = \frac{0}{a} \rightarrow \sin \theta = 0 \rightarrow \theta = 0 $
$ x = a \rightarrow \sin \theta = \frac{a}{a} \rightarrow \sin \theta = 1 \rightarrow \theta = \frac{\pi}{2} $
Bentuk persamaan elips
$ x = 0 \rightarrow \sin \theta = \frac{0}{a} \rightarrow \sin \theta = 0 \rightarrow \theta = 0 $
$ x = a \rightarrow \sin \theta = \frac{a}{a} \rightarrow \sin \theta = 1 \rightarrow \theta = \frac{\pi}{2} $
Bentuk persamaan elips
$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \, $
$ \begin{align} \frac{x^2}{a^2} + \frac{y^2}{b^2} & = 1 \\ \frac{y^2}{b^2} & = 1 - \frac{x^2}{a^2} \\ y^2 & = b^2 - \frac{x^2}{a^2} \times b^2 \\ y^2 & = \frac{b^2 \times a^2}{a^2} - \frac{x^2}{a^2} \times b^2 \\ y^2 & = \frac{b^2}{a^2} ( a^2 - x^2 ) \\ y & = \sqrt{\frac{b^2}{a^2} ( a^2 - x^2 ) } \\ y & = \frac{b}{a} \sqrt{ a^2 - x^2 } \end{align} $
Ingat rumus sudut ganda: $ \cos ^2 \theta = \frac{1}{2} (1 + \cos 2 \theta ) $
Sekarang kita gunakan pembuktian dengan integral:
$\begin{align} \text{Luas } & = 4 \times \text{luas arsiran} \\ & = 4 \times \int \limits_0^a \frac{b}{a} \sqrt{ a^2 - x^2 } dx \, \, \, \, \, \text{(ganti semua dengan } \theta ) \\ & = 4 \times \int \limits_0^\frac{\pi}{2} \frac{b}{a} \times a \cos \theta \times a \cos \theta \, d \theta \\ & = 4 \times \int \limits_0^\frac{\pi}{2} ab \cos ^2 \theta \, d \theta \\ & = 4ab \int \limits_0^\frac{\pi}{2} \cos ^2 \theta \, d \theta \\ & = 4ab \int \limits_0^\frac{\pi}{2} \frac{1}{2} (1 + \cos 2 \theta ) \, d \theta \\ & = 2ab \int \limits_0^\frac{\pi}{2} (1 + \cos 2 \theta ) \, d \theta \\ & = 2ab [\theta + \frac{1}{2}\sin 2 \theta ]_0^\frac{\pi}{2} \\ & = 2ab [(\frac{\pi}{2} + \frac{1}{2}\sin 2 \frac{\pi}{2} ) - (0 + \frac{1}{2}\sin 2 \times 0 ) ] \\ & = 2ab [(\frac{\pi}{2} + \frac{1}{2}\sin \pi ) - (0 + 0 ) ] \\ & = 2ab [(\frac{\pi}{2} + 0 ) - (0 + 0 ) ] \\ & = 2ab [ \frac{\pi}{2} ] \\ & = \pi \times a \times b \end{align} $
Terbukti bukan? kenapa rumus luas elips seperti di atas.
Selanjutnya mari lihat contoh soal dan pembahasan menghitung luas elips berikut ini,
Contoh Soal dan Penyelesaian Menentukan Luas Elips
Soal 1.
Diketahui persamaan elips $ \frac{x^2}{16} + \frac{y^2}{9} = 1 \, $ Hitunglah luasnya!
Pembahasan:
Nilai a dan b dari bentuk umum persamaan elips:
$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \, $$ a^2 = 16 \rightarrow a = 4 $
$ b^2 = 9 \rightarrow b = 3 $
Luas Elips:
$\begin{align} \text{Luas } & = \pi \times a \times b \\ & = \pi \times 4 \times 3 \\ & = 12 \pi \end{align} $
Soal 2:
Diketahui elips dengan persamaan $ \frac{(x-3)^2}{25} + \frac{(y+1)^2}{49} = 1 \, $ . Berapakah luas elips tersebut?
Pembahasan
Nilai a dan b dari bentuk umum persamaan elips:
$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \, $$ a^2 = 49 \rightarrow a = 7 $
$ b^2 = 25 \rightarrow b = 5 $
Luas Elips:
$\begin{align} \text{Luas } & = \pi \times a \times b \\ & = \pi \times 7 \times 5 \\ & = 35 \pi \end{align} $
Soal 3:
Hitunglah luas elips jika diketahui persamaan elips:
$ 2x^2 + 3y^2 -4x + 12y + 8 = 0 \, $
Pembahasan:
Karena bentuk persamaan belum mengarah pada bentuk persamaan umum elips, maka arahkan ke bentuk umum persamaan elips. Caranya dengan menggunakan kuadrat sempurna.
$\begin{align} 2x^2 + 3y^2 -4x + 12y + 8 & = 0 \\ 2x^2 -4x + 3y^2 + 12y + 8 & = 0 \\ 2[x^2 -2x] + 3[y^2 + 4y] + 8 & = 0 \\ 2[(x - \frac{2}{2})^2 - (\frac{2}{2})^2] + 3[(y+\frac{4}{2})^2 - (\frac{4}{2})^2] + 8 & = 0 \\ 2[(x - 1)^2 - (1)^2] + 3[(y+2)^2 - (2)^2] + 8 & = 0 \\ 2[(x - 1)^2 - 1] + 3[(y+2)^2 - 4] + 8 & = 0 \\ 2(x - 1)^2 - 2 \times 1 + 3(y+2)^2 - 3 \times 4 + 8 & = 0 \\ 2(x - 1)^2 - 2 + 3(y+2)^2 - 12 + 8 & = 0 \\ 2(x - 1)^2 + 3(y+2)^2 - 6 & = 0 \\ 2(x - 1)^2 + 3(y+2)^2 & = 6 \\ \frac{2(x - 1)^2 + 3(y+2)^2}{6} & = \frac{6}{6} \\ \frac{(x - 1)^2}{3} + \frac{(y+2)^2}{2} & = 1 \end{align} $
Jadi bentuk persamaan umum elipsnya:
$ x^2 +kx = (x+\frac{k}{2})^2 - (\frac{k}{2})^2 $
Nah selanjutnya lakukan seperti contoh soal sebelumnya dimana anda dapat tentukan nilai:
$ a^2 = 3 \rightarrow a = \sqrt{3} $
$ b^2 = 2 \rightarrow b = \sqrt{2} $
dan Luas elips:
$\begin{align} \text{Luas } & = \pi \times a \times b \\ & = \pi \times \sqrt{3} \times \sqrt{2} \\ & = \sqrt{6} \pi \end{align} $
Jadilah Komentator Pertama untuk "Rumus Luas Elips"
Post a Comment