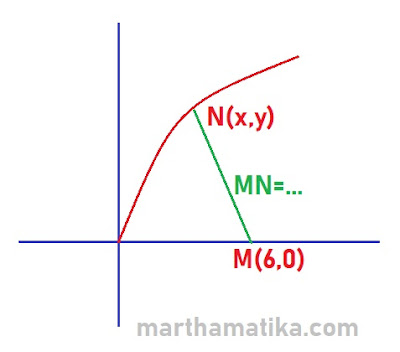
Dasar penyelesainnya adalah dimana diasumsikan sebuah titik pada f(x), anggap itu titik N (x,y). Berdasarkan rumus jarak antara dua titik pada koordinat, MN bisa dihitung:
$ MN= \sqrt {(x-a)^2 + (y-b)^2}$.
Berdasarkan konsep nilai maksimum dan nilai minimum, maka jarak terdekat atau minimum itu terjadi saat $ \frac {d(MN}{dx}=0$ atau turunan pertama fungsi dalam MN=0. Mempermudah pemahaman anda perhatikan contoh soal di bawah ini,
Soal: Jarak terdekat titik (6,0) ke kurva y=2$\sqrt x$ adalah...
Pembahasan:
Berdasarkan rumusan di atas kita ketahui,
(a,b)= (6,0)
Asumsikan ada satu titik pada kurva /grafik y=2$\sqrt x$ yakni (x,y).
$ MN= \sqrt {(x-a)^2 + (y-b)^2} \\ MN= \sqrt {(x-6)^2 + (y-0)^2}$
Subtitusikan y=2$\sqrt x$
$MN= \sqrt {(x-6)^2 + (2\sqrt x-0)^2} \\ MN = \sqrt { x^2-12x+36 +4x} \\ MN = ( x^2-12x+36 +4x)^ {\frac {1}{2}}$
Sesuai syarat maksimum dan minimum dimana terjadi saat turunan pertama =0 maka,
$ \frac {d(MN}{dx}=0 \\ \frac {2x-12+4}{ \sqrt { x^2-12x+36 +4x} } =0 \\ 2x-8 =0 \\ x=4$
Jadi jarak terdekat itu terjadi saat x=4. Silakan disubtitusi ke persamaan:
$MN= \sqrt {(x-6)^2 + (2\sqrt x-0)^2}\\ MN =\sqrt {(4-6)^2 + (2\sqrt 4-0)^2} = 2 \sqrt 5$
Jadilah Komentator Pertama untuk "Cara Menentukan Jarak Terdekat Titik ke Grafik dengan Turunan"
Post a Comment