Contoh Soal dan Pembahasan Luas dan Keliling Irisan 2 Lingkaran

martha yunanda contoh soal, elips dan lingkaran

Sebelumnya, pastikan anda telah membaca konsep dasar dan langkah bagaimana cara mencari luas dan keliling irisan dua lingkaran. Tujuannya, agar anda mudah memahami contoh soal dan pembahasan keliling dan luas area irisan dua lingkaran ini.

Hitunglah Luas dan Keliling daerah Irisan Lingkaran dengan persamaan:
$L_1 : \, (x+2)^2 + (y-1)^2 = 49 \\  L_2 : \, (x-6)^2 + (y-1)^2 = 9$

Langkah 1:
Menentukan jari-jari masing masing Lingkaran,
Berdasarkan persamaan lingkaran di atas, kita ketahui r1 = 7 dan r2 =3.

Langkah 2:
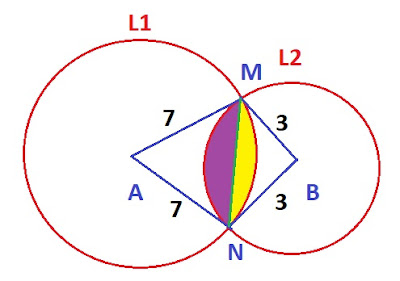
Menentukan titik potong lingkaran dan panjang garis MN pada gambar di atas.
$L_1 : \, (x+2)^2 + (y-1)^2 = 49 \\ dipecah \\ L_1: x^2 + y^2 + 4x -2y -44 = 0 \\ DAN \\ L_2 : \, (x-6)^2 + (y-1)^2 = 9 \\dipecah \\ L_2: x^2 + y^2 -12x -2y + 28 = 0$
Cari titik Potong
Eliminasi kedua persamaan lingkaran :
$\begin{array}{cc} x^2 + y^2 + 4x -2y -44 = 0 & \\ x^2 + y^2 -12x -2y + 28 = 0 & -\\ \hline 16x -72 = 0 & \\ x = 4,5 & \end{array}$
$x = 4,5 \,$ substitusi ke salah satu persamaan lingkaran.
$\begin{align} x = 4,5 \rightarrow (x-6)^2 + (y-1)^2 & = 9 \\ (4,5-6)^2 + (y-1)^2 & = 9 \\ 2,25 + (y-1)^2 & = 9 \\ (y-1)^2 & = 6,75 \\ y -1 & = \pm \sqrt{6,75} \\ y & = 1 \pm \sqrt{6,75} \\ y_1 = 1 -\sqrt{6,75} \vee y_2 & = 1 + \sqrt{6,75} \end{align}$
dan didapat koordinat M ($4,5 ; 1 -\sqrt{6,75}$ ) dan N($4,5 ; 1 + \sqrt{6,75}$)
Panjang garis MN
MN = $\sqrt{(4,5 -4,5 )^2 + [(1 + \sqrt{6,75}) -(1 -\sqrt{6,75}) ]^2 } = 2\sqrt{6,75}$

Langkah 3: 
Menentukan Sudut Pusat ke dua Lingkaran dengan aturan cosinus,

 dan didapat:
Sudut MAN:
$\cos \angle MAN= \frac{71}{98} \\ \angle MAN  = arc \, \cos \frac{71}{98} \\ \angle MAN  = 43,57^\circ = 44^\circ$

Sudut MBN
$\cos \angle MBN  = \frac{-1}{2} \\ \angle MBN  = arc \, \cos \frac{-1}{2} \\ \angle MBN  = 120^\circ$

Langkah 4:
a) Keliling
 Busur MN pada L1:
$MN =  \frac{\angle MAN}{360^\circ} . 2 \pi . r_1  \\ MN = \frac{44^\circ}{360^\circ} . 2 \frac{22}{7} . 7 \\ MN  = 5,38$

Busur MN pada L2
 $MN = \frac{\angle MBN}{360^\circ} . 2 \pi . r  \\ MN =  \frac{120^\circ}{360^\circ} . 2 \frac{22}{7} . 3 \\ MN =  6,29$

Keliling total = 5,38 + 6,29 = 11,67

b) Luas Irisan 2 Lingkaran

 $Juring \, AMN = \frac{\angle MAN}{360^\circ} . \pi . r_1^2 \\ Juring \, AMN= \frac{44^\circ }{360^\circ} . \frac{22}{7} . 7^2 \\ Juring \, AMN = 21,39$
$\triangle AMN =  \frac{1}{2}. AM . AN. \sin \angle MAN \\ \triangle AMN = \frac{1}{2}.7^2 . \sin 44^\circ \\ \triangle AMN = 17,02$
Tembereng 1 (kuning) = Juring AMN - Segitiga AMN = 21,39 -17,02 = 4,37.

$Juring \, MBN=  \frac{\angle MBN}{360^\circ} . \pi . r_2^2 \\ Juring \, MBN = \frac{120^\circ }{360^\circ} . \frac{22}{7} . 3^2  \\ Juring \, MBN = 9,43$
$\triangle MBN = \frac{1}{2}. BC . BD. \sin \angle CBD \\ \triangle MBN = \frac{1}{2}.3^2 . \sin 120^\circ  \\ \triangle MBN = 3,89$
Tembereng 2 (ungu) =  Juring MBN - segitiga MBN=9,43 -3,89 = 5,54.

Luas total =Tembereng 1 (kuning) +Tembereng 2 (ungu) 
Luas total = 4,37 + 5,54 = 9,91

Share on Facebook

Share on Twitter

Share on LinkedIn