Menentukan Proyeksi Titik, Garis, dan Bidang

martha yunanda geometri

Penjelasan proyeksi dalam matematika adalah percerminan proyeksian pada proyeksitor. Hasil proyeksi berada pada proyeksitor. Apabila proyeksian dan hasil proyeksi dihubungkan maka akan saling tegak lurus. Hasil proyeksi akan sama dengan apa yang diproyeksikan. Jika anda proyeksikan titik maka hasilnya akan titik, jika anda proyeksikan garis maka hasilnya akan garis.

Istilah istilah di atas bisa didefenisikan,

1. Proyeksian : Objek yang akan diproyeksikan
2. Proyeksitor : tujuan atau tempat dimana proyeksian akan diproyeksikan
3. Hasil proyeksi : Hasil (bayangan) proyeksian pada proyeksitor.

Agar memudahkan anda dalam memahami, berikut silakan dilihat,

Proyeksi Titik pada Garis

Telah disinggung di atas. jika sebuah titik diproyeksikan maka hasilnya tetap berupa titik. Perhatikan contoh proyeksi titik pada gambar di bawah ini,

Titik P diproyeksikan terhadap garis AB. Hasilnya yaitu P'. Titik P disebut dengan proyeksian, Proyeksitor adalah garis AB dan hasil proyeksi adalah titik P'. Jelas terlihat adanya,garis PP' (antara proyeksian dan hasil proyeksi) tegak lurus terhadap proyeksitor.

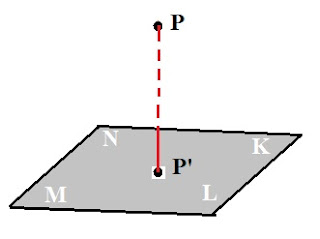
Proyeksi Titik pada Bidang

Sementara untuk proyeksi pada bidang tidak jauh berbeda dengan proyeksi titik pada garis. Bisa diperhatikan ilustrasi di bawah ini.

Anda tentu bisa menyebutkan masing masingmana proyeksitor, proyeksian dan hasil proyeksian.

Proyeksi Garis ke Garis

Ilustrasi untuk proyeksi garis ke garis sebagai berikut

Diproyeksikan garis PQ pada garis k. Garis PQ adalah Proyeksian, garis k proyeksitor dan garis P'Q' adalah hasil proyeksian. Kuncinya dalam memproyeksikan garis, adalah proyeksikan titik ujung ruas garis masing masing pada bidang proyeksi.

Proyeksi Garis pada Bidang

Silakan dianalisa dan tentukan mana yang proyeksian, proyeksitor dan hasil proyeksi.

Proyeksi Bidang pada Bidang

Proyeksinya sama saja dimana diproyeksikan titik titik sudut pada bidang masing masing pada proyeksitor. Kemudian hubungkan titik hasil proyeksi tersebut sehingga terbentuk bidang baru.

Contoh Soal Proyeksi Garis titik, bidang dan garis

Diketahui kubus ABCD.EFGH. Tentukan hasil proyeksi dalam bentuk gambar dari:

1. titik A ke garis FH
2. titik A ke bidang CDH
3. garis AH ke garis AD
4. garis AE ke bidang AFH
5. bidang AFH ke bidang ABCD

Jawab:

No	Proyeksian	Proyeksitor	Hasil Proyeksi
1	A	FH	A’
2	A	CDH	A’=D
3	AH	AD	A’H’=AD
4	AE	AFH	AP
5	AFH	ABCD	ABD

Share on Facebook

Share on Twitter

Share on LinkedIn